Lagrangian points are well known to anybody interested in astronomy or astrophysics. But even if you are not into the science part of SF, chances are you came across them in fiction anyway – because they are quite a good trope to exploit.
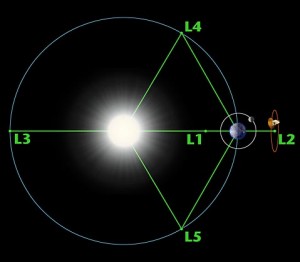
Lagrange points are named in honor of Joseph-Louis Lagrange, who brilliantly prepared a solution for the mathematical problem, known as the “General Three-Body Problem”, in his now famous paper (Essai sur le Problème des Trois Corps, 1772). Simply put, there are five special points where a body between two larger masses can orbit in a constant pattern. This is because in these special positions the gravitational pull of two large masses equals the centripetal force required for a small object to move along.
It has to be mentioned that not all the five L points enjoy the same stability. Actually, three of them are rather unstable, namely L1, L2 and L3, which all lie along the line connecting the two large masses. It does not matter a big deal for our uses, though: NASA and other space agencies regularly use the ones on Sun-Earth orbit. For example, L1 point allows an uninterrupted view of the sun and therefore the Solar and Heliospheric Observatory Satellite SOHO is set there. L2 is another quite busy point. In the words of NASA, it is “ideal for astronomy because a spacecraft is close enough to readily communicate with Earth, can keep Sun, Earth and Moon behind the spacecraft for solar power and (with appropriate shielding) provides a clear view of deep space for our telescopes.” Unsurprisingly, it was the first home to the WMAP spacecraft, now to Planck, and to the James Webb Space Telescope in future.
L3 is of no use to science – simply because it remains hidden behind the Sun at all times (more on this one when discussing SF). L4 and L5 are instead stable points, meaning that they don’t need external source of power (ie, rockets) for course and attitude corrections. Unsurprisingly, there’s where a lot of asteroids are located in the Solar System, like the Trojans on the Jupiter-Sun orbit.
How to locate Lagrangian points? Adopting a frame of reference that rotates with the system is the easiest way to do it. As shown below, the forces are at their peak when the contours are closest together and weakest when the contours are far apart.
A good explanation of the mathematics and the physics behind the Lagrangian points can be found here. I do also advise, in case you want to watch an entertaining, and yet very accurate, video about them and their possible present and future uses, to have a look at this one, done by Artifexian.
Finally, while so far space agencies have only exploited the Sun-Earth orbit, they have given some thoughts to the five L points in the Earth-Moon system, especially to the two stable points L4 and L5 of the Moon’s orbit. These positions have been studied as possible sites for artificial space colonies. And this leads us to discuss the use of Lagrangian points in fiction, the topic of my next post.
2 Comments